925. Perimeter
and area of triangle
Six real numbers x1, y1,
x2, y2, x3,
y3 – the coordinates of
triangle vertices are given. Find the perimeter and the area of a triangle.
Input. Six real numbers – the
coordinates of triangle vertices are given: x1, y1, x2, y2,
x3, y3. The
numbers do not exceed 100 by absolute value.
Output. Print the
perimeter and the area of a triangle with 4 decimal digits.
|
Sample
input |
Sample
output |
|
3 2 7 6.5 10
1 |
19.3568
17.7500 |
SOLUTION
geometry
Algorithm analysis
Given the
coordinates of triangle vertices, first find the lengths of its sides. Next, compute the perimeter
as the sum of the sides lengths and the area according to Heron’s formula.
The
area of triangle ABC, given with
coordinates of its vertces A(x1, y1), B(x2,
y2), C(x3,y3), is
S = ![]() abs
abs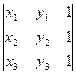
Subtract the first line from the second and third lines and compute the determinant using the third column:
S = ![]() abs
abs =
= ![]() abs
abs =
=
![]() | (x2 – x1) * (y3 – y1)
– (x3 – x1) * (y2 – y1)
|
| (x2 – x1) * (y3 – y1)
– (x3 – x1) * (y2 – y1)
|
Algorithm realization
Read
the input data.
scanf("%lf %lf %lf %lf %lf
%lf",&xx1,&yy1,&xx2,&yy2,&xx3,&yy3);
Calculate the lengths of the sides
of a triangle a, b, c.
a = sqrt((xx2 - xx1)*(xx2 - xx1) + (yy2 - yy1)*(yy2 - yy1));
b = sqrt((xx3 - xx1)*(xx3 - xx1) + (yy3 - yy1)*(yy3 - yy1));
c = sqrt((xx3 - xx2)*(xx3 - xx2) + (yy3 - yy2)*(yy3 - yy2));
Find the perimeter p and
semiperimeter pp of triangle.
p = a + b + c; pp = p / 2;
The area of the triangle is
calculated using Heron’s
formula.
s = sqrt(pp * (pp - a) * (pp - b) * (pp - c));
Print the perimeter and the
area of triangle with the given accuracy.
printf("%.4lf %.4lf\n",p,s);
Algorithm realization – determinant
#include <stdio.h>
#include <math.h>
double xx1, yy1, xx2, yy2, xx3, yy3;
double a, b, c, p, s;
double TriangleArea(double x1, double y1, double x2, double y2,
double x3, double y3)
{
return fabs((x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)) /
2.0;
}
int main(void)
{
scanf("%lf %lf %lf %lf %lf %lf", &xx1, &yy1, &xx2, &yy2, &xx3, &yy3);
a = sqrt((xx2 - xx1) * (xx2 - xx1) + (yy2 -
yy1) * (yy2 - yy1));
b = sqrt((xx3 - xx1) * (xx3 - xx1) + (yy3 -
yy1) * (yy3 - yy1));
c = sqrt((xx3 - xx2) * (xx3 - xx2) + (yy3 -
yy2) * (yy3 - yy2));
p = a + b + c;
s = TriangleArea(xx1, yy1, xx2, yy2, xx3,
yy3);
printf("%.4lf %.4lf\n", p,
s);
return 0;
}
Algorithm realization – class triangle
#include <stdio.h>
#include <math.h>
class Triangle
{
private:
double x[3], y[3];
double a, b, c;
public:
Triangle(void)
{
scanf("%lf %lf %lf %lf %lf %lf",&x[0],&y[0],&x[1],&y[1],&x[2],&y[2]);
a = sqrt((x[1] -
x[0])*(x[1] - x[0]) + (y[1] - y[0])*(y[1] - y[0]));
b = sqrt((x[2] -
x[0])*(x[2] - x[0]) + (y[2] - y[0])*(y[2] - y[0]));
c = sqrt((x[2] -
x[1])*(x[2] - x[1]) + (y[2] - y[1])*(y[2] - y[1]));
}
double Perimeter(void)
{
return a + b + c;
}
double Area(void)
{
double p = Perimeter() / 2;
return sqrt(p * (p - a) * (p - b) * (p - c));
}
};
int main(void)
{
Triangle tri;
printf("%.4lf %.4lf\n",tri.Perimeter(),tri.Area());
return 0;
}
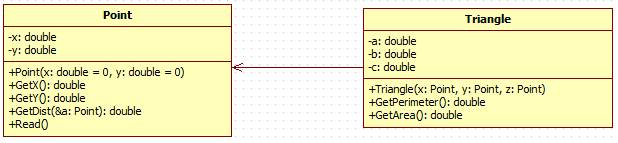
Algorithm realization – two
classes
#include <stdio.h>
#include <math.h>
class Point {
public:
Point(double
x, double y);
double
GetX();
double
GetY();
double
GetDist(Point &a);
void Read();
private:
double x;
double y;
};
Point::Point(double x = 0, double
y = 0) {
this->x =
x;
this->y =
y;
}
double Point::GetX() {
return x;
}
double Point::GetY() {
return y;
}
double Point::GetDist(Point &a) {
return sqrt((this->x - a.GetX()) * (this->x
- a.GetX()) +
(this->y - a.GetY())*(this->y - a.GetY()));
}
void Point::Read() {
scanf("%lf %lf",&x,&y);
}
class Triangle {
public:
Triangle(Point x, Point y, Point z);
double
GetPerimeter();
double GetArea();
private:
double a;
double b;
double c;
};
Triangle::Triangle(Point
x, Point y, Point z) {
a = x.GetDist(y);
b = y.GetDist(z);
c = z.GetDist(x);
}
double Triangle::GetPerimeter() {
return a + b
+ c;
}
double Triangle::GetArea() {
double p =
GetPerimeter() / 2;
return sqrt(p
* (p - a) * (p - b) * (p - c));
}
int main(void)
{
Point A, B, C;
A.Read();
B.Read();
C.Read();
Triangle tri(A,B,C);
printf("%.4lf
%.4lf\n",tri.GetPerimeter(),tri.GetArea());
return 0;
}
Java realization
import java.util.*;
public class Main
{
public static void
main(String []args)
{
Scanner con = new Scanner(System.in);
double x1 = con.nextDouble(),
y1 = con.nextDouble();
double x2 = con.nextDouble(),
y2 = con.nextDouble();
double x3 = con.nextDouble(),
y3 = con.nextDouble();
double a =
Math.sqrt((x2 - x1)*(x2 - x1) + (y2 - y1)*(y2 - y1));
double b =
Math.sqrt((x3 - x1)*(x3 - x1) + (y3 - y1)*(y3 - y1));
double c =
Math.sqrt((x3 - x2)*(x3 - x2) + (y3 - y2)*(y3 - y2));
double p = a + b + c, pp = p / 2;
double s =
Math.sqrt(pp * (pp - a) * (pp - b) * (pp - c));
System.out.printf("%.4f
%.4f\n",p,s);
con.close();
}
}
Java realization – class triangle
import java.util.*;
class Triangle
{
double x[], y[];
double a, b, c;
public
Triangle()
{
x = new double[3];
y = new double[3];
Scanner con = new
Scanner(System.in);
x[0] =
con.nextDouble(); y[0] =
con.nextDouble();
x[1] =
con.nextDouble(); y[1] =
con.nextDouble();
x[2] =
con.nextDouble(); y[2] =
con.nextDouble();
a =
Math.sqrt((x[1] - x[0])*(x[1] -
x[0]) + (y[1] - y[0])*(y[1] -
y[0]));
b =
Math.sqrt((x[2] - x[0])*(x[2] -
x[0]) + (y[2] - y[0])*(y[2] -
y[0]));
c =
Math.sqrt((x[2] - x[1])*(x[2] -
x[1]) + (y[2] - y[1])*(y[2] -
y[1]));
con.close();
}
public double
Perimeter()
{
return a + b + c;
}
public double
Area()
{
double p =
Perimeter() / 2;
return
Math.sqrt(p * (p - a) * (p - b) * (p - c));
}
}
public class Main
{
public static void
main(String []args)
{
Triangle tri = new
Triangle();
System.out.printf("%.4f
%.4f\n", tri.Perimeter(),tri.Area());
}
}
Java realization – class triangle
import java.util.*;
class Triangle
{
double a, b, c;
public Triangle(double x[], double y[])
{
a =
Math.sqrt((x[1] - x[0])*(x[1] -
x[0]) + (y[1] - y[0])*(y[1] -
y[0]));
b = Math.sqrt((x[2] -
x[0])*(x[2] - x[0])
+ (y[2] - y[0])*(y[2] -
y[0]));
c =
Math.sqrt((x[2] - x[1])*(x[2] -
x[1]) + (y[2] - y[1])*(y[2] -
y[1]));
}
public double
Perimeter()
{
return a + b + c;
}
public double
Area()
{
double p = Perimeter()
/ 2;
return
Math.sqrt(p * (p - a) * (p - b) * (p - c));
}
}
public class Main
{
public static void
main(String []args)
{
Scanner con = new
Scanner(System.in);
double x[] = new double[3];
double y[] = new double[3];
x[0] =
con.nextDouble(); y[0] =
con.nextDouble();
x[1] =
con.nextDouble(); y[1] =
con.nextDouble();
x[2] =
con.nextDouble(); y[2] =
con.nextDouble();
Triangle tri = new
Triangle(x,y);
System.out.printf("%.4f
%.4f\n",tri.Perimeter(),tri.Area());
con.close();
}
}
Java realization – classes point, triangle
import java.util.*;
class Point
{
private double x, y;
Point()
{
x = y = 0;
}
Point(double x, double y)
{
this.x = x;
this.y = y;
}
public double GetDistance(Point a)
{
return Math.sqrt((this.x - a.x)*(this.x - a.x) + (this.y - a.y)*(this.y - a.y));
}
};
class Triangle
{
double a, b, c;
public
Triangle(Point a, Point b,
Point c)
{
this.a = a.GetDistance(b); //
a = AB
this.b = b.GetDistance(c); //
b = BC
this.c = c.GetDistance(a); //
c = AC
}
public double
Perimeter()
{
return a + b + c;
}
public double
Area()
{
double p =
Perimeter() / 2;
return
Math.sqrt(p * (p - a) * (p - b) * (p - c));
}
}
public class Main
{
public static void
main(String []args)
{
Scanner con = new
Scanner(System.in);
Point a = new
Point(con.nextDouble(), con.nextDouble());
Point b = new
Point(con.nextDouble(), con.nextDouble());
Point c = new
Point(con.nextDouble(), con.nextDouble());
Triangle tri = new
Triangle(a,b,c);
System.out.printf("%.4f
%.4f\n",tri.Perimeter(),tri.Area());
con.close();
}
}
Python realization
import math
x1,y1,x2,y2,x3,y3 = map(float,input().split())
a = math.sqrt((x2
- x1) * (x2 - x1) + (y2 - y1) * (y2 - y1));
b = math.sqrt((x3
- x1) * (x3 - x1) + (y3 - y1) * (y3 - y1));
c = math.sqrt((x2
- x3) * (x2 - x3) + (y2 - y3) * (y2 - y3));
p = a + b + c
sp = p / 2
s = math.sqrt(sp * (sp - a) * (sp - b) * (sp - c));
print(p, s)